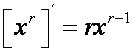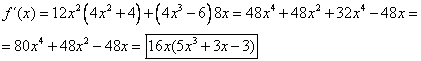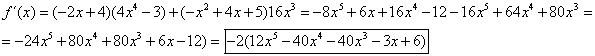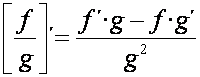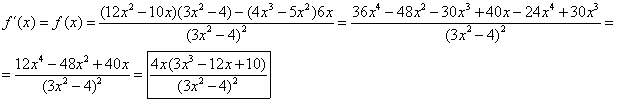dominio de funciones Raiz de Polinomio

FUNCIONES

¿Qué es una función?

Una función es como una máquina: tiene una entrada y una salida. Y lo que sale está relacionado de alguna manera con lo que entra.

Ejemplos

• "Multiplicar por 2" es una función muy simple
• La raíz cuadrada (√) es una función
• Seno, coseno y tangente son funciones que se usan en trigonometría

... ahora vamos a ver la idea general de una función.

Nombres

Primero, es útil darle un nombre a una función. El nombre más común es "f", pero puedes ponerle otros como "g" ... o hasta "mermelada" si quieres.

Y también está bien darle nombre a lo que se va adentro de la función, se pone entre paréntesis () después del nombre de la función:

Así que f(x) te dice que la función se llama "f", y "x" se pone dentro

Y normalmente verás lo que la función hace a la entrada:

f(x) = x² nos dice que la función "f" toma "x" y lo eleva al cuadrado.

Así que con la función "f(x) = x²", una entrada de 4 da una salida de 16. De hecho podemos escribir f(4) = 16.

A veces las funciones no tienen nombre, y puede que veas algo como y = x²

¿Con qué tipo de cosas trabaja una función?

Los "números" parecen una respuesta clara, pero...

	... ¿qué números? Por ejemplo, la función de la altura del árbol a(edad) = edad×20 no tiene sentido si la edad es menor que cero.
	... también podrían ser letras ("A"→"B"), o códigos de identificación ("A6309"→"Acceso") o cosas más raras.

Así que tenemos que usar algo más general, y ahí es donde entran en juego los conjuntos:

Un conjunto es una colección de cosas, por ejemplo números. Aquí tienes algunos ejemplos: El conjunto de los números pares: {..., -4, -2, 0, 2, 4, ...} Un conjunto de ropa: {"sombrero","camisa",...} El conjunto de los números primos: {2, 3, 5, 7, 11, 13, 17, ...} Los múltiplos de 3 que son más pequeños que 10: {3, 6, 9} Cada cosa individual en un conjunto (como "4" o "sombrero") es unmiembro, o elemento.

Así que una función toma elementos de un conjunto, y devuelve (normalmente con algún cambiados) elementos de un conjunto. Con esto llegamos a la definición formal:

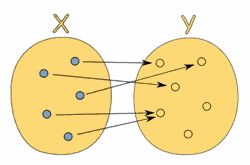Definición formal de función Una función relaciona cada elemento de un conjunto con un elemento exactamente de otro conjunto (puede ser el mismo conjunto).

	"exactamente uno" significa que la función es univaluada. No devolverá 2 o más resultados para la misma entrada. ¡Así que "f(2) = 7 o 9" no vale!
	Cada elemento de "X" se relaciona con un elemento de "Y". Decimos que la función cubre"X" (relaciona cada elemento de)

También fíjate que en el dibujo de arriba hay dos elementos en "X" que se relacionan con el mismo elemento de "Y". No pasa nada. No hay ninguna regla contra esto.

Y finalmente, fíjate en que algunos elementos de "Y" no se relacionan con nada. Eso también vale.

Esto son cosas normales entre funciones, pero algunos tipos de funciones cumplen reglas más estrictas, para saber más lee sobre inyectivo, sobreyectivo y biyectivo

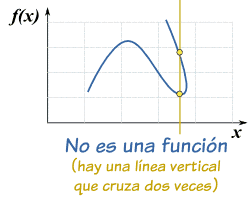La prueba de la línea vertical En un gráfico, la idea de univaluada significa que ninguna línea vertical cruza más de una vez. Si alguna cruzara más de una vez no sería una función.

Dominio, codominio y rango

En el dibujo de arriba

• el conjunto "X" es el dominio,
• el conjunto "Y" es el codominio, y
• el conjunto de elementos de Y a los que llega alguna flecha (los valores verdaderos de la función) se llamarango o imagen.

Tenemos una página especial sobre dominio, codominio y rango por si quieres saber más.

Pares ordenados

Puedes escribir las entradas y salidas de una función como "pares ordenados", como (4,16).

Se llaman pares ordenados porque la entrada siempre va primero y la salida después.

Así que (4,16) significa que la función toma "4" y devuelve "16"

Y una función se puede definir como un conjunto de pares ordenados:

Ejemplo: {(2,4), (4,5), (7,3)} es una función que dice que "2 se relaciona con 4", "4 se relaciona con 5" y "7 se relaciona con 3".


Fíjate también en que el dominio es {2,4,7} y el rango es {4,5,3}

Pero la función debe ser univaluada, esto se puede decir

"si contiene (a, b) y (a, c), entonces b tiene que ser igual a c"

Es otra manera de decir que una entrada "a" no puede dar dos resultados diferentes.

Ejemplo: {(2,4), (2,5), (7,3)} no es una función porque {2,4} y {2,5} quieren decir que 2 estaría relacionado con 4 y 5, o sea no es univaluada

Conclusión

• una función relaciona entradas con salidas
• una función toma elementos de un conjunto (el dominio) y los relaciona con elementos de un conjunto (el codominio).
• las salidas (los verdaderos valores de la función) se llaman la imagen o rango
• una entrada sólo produce una salida (no una u otra)
• una entrada y la salida que corresponde se llaman juntos un par ordenado
• así que una función también se puede ver como un conjunto de pares ordenados

DOMINIO DE FUNCIONES

POLINOMICAS

  

DERIVADA

El concepto se derivada se aplica en los casos donde es necesario medir la rapidez con que se produce el cambio de una situación. Por ello es una herramienta de cálculo fundamental en los estudios de Física, Química y Biología. También en las ciencias sociales como la Economía y la Sociología  se utiliza el análisis matemático para explicar la rapidez de cambio en las  magnitudes que les son propias.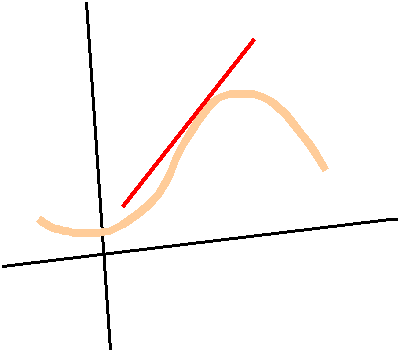

Conocer la variación de una función en un intervalo grande no informa suficientemente bien en el sentido de entender como se produce dicha variación. Se necesita estudiar variaciones de la función en intervalos cada vez más pequeños para llegar a entender el concepto de variación instantánea o referida a un punto, es decir el de derivada en un punto.

Un hallazgo importante en el estudio de la derivada  de una función es que la pendiente o inclinación de la recta tangente a la curva en un punto representa la rapidez de cambio instantáneo. Así pues cuanto mayor es la inclinación de la recta tangente en un punto mayor es la rapidez de cambio del valor de la función en las proximidades del punto.

El concepto de derivada segunda  de una función - derivada de la derivada de una función- también se aplica para saber si la rapidez de cambio se mantiene, aumenta o disminuye. Así el concepto de convexidad y concavidad -aspectos geométricos o de forma- de una función están relacionados con el valor de la derivada segunda.

La derivabilidad de una función en un punto (propiedad relativa a la existencia de tangente en un punto) está asociado al de continuidad. Este aspecto también será tratado en esta unidad.

Finalmente veremos la relación que tiene la derivada  con los problemas de optimización de funciones. Estos problemas decimos que son de máximo o de mínimo (máximo rendimiento, mínimo coste, máximo benefício, mínima aceleración, mínima distancia, etc).

DERIVADA DE UNA FUNCIÓN (DEFINICIÓN)
Dada una función y=f(x) y un punto de abcisa x=a, se define la derivada de f(x) en x=a y se designa f '(a), como el límite siguiente, si es que existe,

y representa desde le punto de vista geométrico la pendiente de la recta tangente a la gráfica de la función y = f(x) en el punto de abcisa x=a.

REGLAS DE DERIVACIÓN

El proceso descrito anteriormente es conocido como derivada por definición, podemos encontrar estos resultados empleando una síntesis de los resultados:

LA DERIVADA DE UNA CONSTANTE es cero. 

Ejercicio nº 1)   Sol:   Ejercicio nº 2)   Sol:   Ejercicio nº 3) Sol:   Ejercicio nº 4) Sol: Ejercicio nº 5)   Sol:   Ejercicio nº 6) Sol: Ejercicio nº 7) Sol: Ejercicio nº   Sol:   Ejercicio nº 9) Sol:

Derivada de una función potencial: Forma simple

LA DERIVADA DE UNA FUNCIÓN POTENCIAL es igual al exponente por la variable elevado a una unidad menos.

Ejercicio nº 10)  Sol: Ejercicio nº 11) Sol: Ejercicio nº 12) Sol :  Ejercicio nº 13) Sol:   Ejercicio nº 14)   Sol:   Ejercicio nº 15)   Sol:

LA DERIVADA DE UNA SUMA DE FUNCIONES es igual a suma de las derivadas de las funciones

Ejercicio nº 16)  Solución:  Ejercicio n°17 Solución Ejercicio n° 18 Solución Ejercicio n°19  Solución:   Ejercicio n°20  Solución Ejercicio n° 21  Solución Ejercicio n°22 Solución Ejercicio n°23 Solución

LA DERIVADA DE UN PRODUCTO DE FUNCIONES es igual a la derivada de la primera función por la segunda función menos la primera función por la derivada de la segunda función

Ejercicio nº 24)  Solución: Ejercicio nº 25)  Solución:   Ejercicio nº 26)  Solución:   Ejercicio nº 27)  Solución:

LA DERIVADA DE UN COCIENTE DE FUNCIONES  es igual a la derivada de la función del numerador por la función del denominador menos la función del numerador por la derivada de la función del denominador, dividido todo ello por el denominador al cuadrado

Ejercicio nº 28)  Solución:   Ejercicio nº 29)  Solución:   Ejercicio nº 30)  Solución:   Ejercicio nº 31)  Solución:   Ejercicio nº 32)  Solución: