Como primer paso no aprenderemos las reglas siguientes:
Veamos algunos ejemplos básicos:
Ejemplo# 1
debe considerar 5x como si fuera la u de la formula asi que u' (la derivada) es 5, la derivada de sen u es u'cos u.
Ejemplo# 2
Considere 3x^2 como si fuese u, la derivada es 6x, y la derivada del cos u es -u'sen u.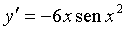
Ejemplo# 3
u' =4, porque u=4x + 5, la derivada de cot u es -u'csc^2u
Ejemplo# 4
igual que los ejemplos anteriores x^3 lo consideramos como u, entonces u' =3x^2. La derivada de sec u es u' secu tanu
Ahora las reglas empleadas para realizar derivadas de sumas, restas producto y cocientes son igualmente aplicadas.
Ejemplo # 5
considere f como x^2 y g cosx, tendriamos el producto, derivando f' = 2x derivavdo g'=-senxy aplicando el producto fg' + gf' obtenemos
PARA FUNCIONES EXPONENCIALES LA DERIVADA ESTA DADA POR:
Aqui la clave esta en tomar la u como el exponente, derivarlo y aplicar la regla presentada para la exponencial.veamos el Ejemplo# 6
la u será 3x^2 + 1, la derivada es 6x, la parte de la exponencial queda igual, entonces la derivada es
PARA FUNCIONES LOGARITMICA LA DERIVADA ESTA DADA POR:
Ilustraremos con el siguiente ejemplo:Ejemplo# 7
aclaramos que en L corresponde a ln, asi que la derivada la obtenemos asi. consideremos u como x^2+7x, u' seria 2x + 7 y la derivada del ln es
Para obtener destreza en este tema es necesario practicar, a continuación te presentamos el siguiente vinculo para que desarrolles la práctica.http://www.thatquiz.org/es/classtest?qwqt5120
